Introduktion
Der er en bred vifte af tekniske analyseværktøjer (TA) og indikatorer, som handlende kan bruge til at forsøge at forudsige fremtidige prisudviklinger. Disse kan omfatte komplette markedsanalyserammer såsom Wyckoff-metoden, Elliott Wave Theory eller Dow Theory. De kan også være indikatorer såsom glidende gennemsnit, relativt styrkeindeks (RSI), stokastisk RSI, Bollinger Bands, Ichimoku Clouds, parabolsk SAR eller MACD.
Fibonacci retracement-værktøjet er en populær indikator, der bruges af tusindvis af handlende på aktiemarkederne, valutamarkedet og kryptovalutamarkederne. Fascinerende nok er den baseret på Fibonacci-sekvensen, der blev opdaget for mere end 700 år siden.
Denne artikel vil gennemgå, hvad Fibonacci retracement-værktøjet er, og hvordan du kan bruge det til at finde vigtige niveauer på en graf.
Hvad er Fibonacci retracement?
Fibonacci retracement (eller Fib retracement) er et værktøj, der bruges af tekniske analytikere og handlende i et forsøg på at forudsige interesseområder på en graf. Det gør de ved at bruge Fibonacci-forhold som procenter. Fib retracement-værktøjet er afledt af en række tal identificeret af matematikeren Leonardo Fibonacci i det 13. århundrede. Denne talrække kaldes Fibonacci-sekvensen. Visse matematiske forhold mellem tal i denne sekvens skaber forhold, der derefter afbildes til en graf. Disse forhold er:
0 %
23,6 %
38,2 %
61,8 %
78,6 %
100 %
Selvom det teknisk set ikke er et Fibonacci-forhold, anser nogle handlende også 50 %-niveauet for at have en vis betydning, da det repræsenterer midtpunktet i prisklassen. Fibonacci-forhold uden for 0-100 %-området kan også anvendes, f.eks. 161,8 %, 261,8 % eller 423,6 %.
Vi vil gennemgå, hvordan handlende kan bruge disse procentdele, men hovedpointen er, at de niveauer, der er skitseret af dem, kan korrelere med betydelige niveauer på markedet. Når fibonacci-niveauerne plottes på en prisgraf, kan de bruges til at identificere interesseområder såsom støtte, modstand, retracement-områder, indgangspunkter, udgangsmål og stop-loss-niveauer.
Sådan beregnes Fibonacci retracement
Eftersom disse procenter er de samme i alle Fibonacci retracement-værktøjer, behøver du ikke manuelt at beregne noget. Måden at få dem på er dog at starte med Fibonacci-numrene.
Lad os oprette en sekvens af tal, der starter med nul og en, og fortsætte med at føje summen af de to foregående tal til den aktuelle. Hvis vi fortsætter dette på ubestemt tid, får vi en talrække, der kaldes Fibonacci-sekvensen.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ... og så videre. Disse tal er selvfølgelig ikke direkte plottet på en prisgraf. Men de niveauer, der anvendes i Fibonacci retracement-værktøjet, er alle afledt af disse tal på én eller anden måde.
Hvis du ser bort fra de første par tal, og dividerer et tal med det tal, der følger det, får du altid et forhold tæt på 0,618. Hvis du f.eks. dividerer 21 med 34, får du 0,6176. Og hvis du dividerer et tal med det tal, der står to pladser til højre, får du et forhold tæt på 0,382. Hvis du f.eks. deler 21 med 55, får du 0,3818. Alle forholdene (undtagen 50 %) i Fibonacci retracement-værktøjet er baseret på nogle beregninger, der involverer denne metode.
Fibonacci-sekvensen og det gyldne snit
Som nævnt blev Fibonacci-sekvensen identificeret af matematikeren Leonardo Fibonacci i det 13. århundrede. Det gyldne snit (0,618 % eller 1,618 %) er et matematisk forhold, der er afledt af disse tal. Men hvorfor er det så vigtigt et tal?
Det gyldne snit beskriver proportionerne af en forbløffende lang liste over fænomener i universet og kan findes overalt i naturen. Tænk på atomer, stjerner, galakseformationer, skaller, selv honningbier – alt fra det mindste til det største kan vise eksempler på denne proportion.
Endvidere er det blevet brugt af kunstnere, ingeniører og designere i århundreder til at skabe æstetisk tiltalende kompositioner. Fra pyramiderne til Mona Lisa og Twitter-logoet – mange berømte kunstværker og design bruger det gyldne snit på én eller anden måde. Og det viser sig, at dette snit også kan have betydning på de finansielle markeder.
Sådan bruges Fibonacci retracement
Nu hvor vi ved, hvad Fibonacci retracement-værktøjet er, og hvordan det fungerer, så lad os overveje dets anvendelse som et værktøj på de finansielle markeder.
Typisk trækkes værktøjet mellem to væsentlige prispunkter såsom et højdepunkt og et lavpunkt. Dette interval bruges derefter som grundlag for yderligere analyse. Normalt bruges værktøjet til at kortlægge niveauer inden for intervallet, men det kan også give indsigt i vigtige prisniveauer uden for intervallet.
Typisk trækkes dette interval i henhold til den underliggende tendens. Så i en opadgående tendens ville lavpunktet være 1 (eller 100 %), mens højdepunktet ville være 0 (0 %). Ved at tegne Fib retracement-linjer over en opadgående tendens kan handlende få en idé om potentielle støtteniveauer, der kan testes, hvis markedet begynder at gå tilbage ("retrace") – deraf udtrykket retracement.

Omvendt ville lavpunktet under en nedadgående tendens være 0 (0 %) og højdepunktet 1 (100 %). Bemærk, at prisen er i en nedadgående tendens. Så retracementet refererer i dette tilfælde til bevægelsen fra bunden (et spring). I denne sammenhæng kan Fibonacci retracement-værktøjet give indblik i potentielle modstandsniveauer, hvis markedet begynder at bevæge sig op.

Hvad Fibonacci-niveauer fortæller handlende
Handlende kan bruge Fibonacci-niveauer til at bestemme potentielle indgangsområder, prismål eller stop-loss-punkter. Dette kan variere betydeligt i den enkelte opsætning, strategi og handelsstil.
Nogle strategier involverer at drage fordel af intervallet mellem to specifikke Fibonacci-niveauer. Overvej f.eks. en opadgående tendens efterfulgt af en retracement. At købe på 38,2 % retracement-niveauet og derefter sælge på 23,6 %-niveauet kunne være en interessant strategi. Dette afhænger naturligvis meget af individuel strategi og mange andre tekniske faktorer.
Fibonacci-niveauer kombineres desuden ofte med Elliott Wave Theory for at finde sammenhænge mellem bølgestrukturer og potentielle interesseområder. Dette kan være en effektiv strategi til at forudsige omfanget af retracements i forskellige bølger af en bestemt markedsstruktur.
Som med andre teknikker er Fibonacci retracement-værktøjet mest effektivt, når det kombineres med andre tekniske analyseindikatorer. Hvad der måske ikke er et købs- eller salgssignal i sig selv, kan blive til et, hvis det bekræftes af andre indikatorer. Som sådan, hvis prisen rammer et bestemt Fibonacci-niveau, kan det være den vender, eller ej. Derfor er det vigtigt at styre risikoen, samtidig med at man tager hensyn til markedsmiljøet og andre faktorer.
Fibonacci-udvidelser
Som nævnt kan Fibonacci-niveauerne bruges til at evaluere retracement- eller bounce-områder (nummer 1 i animationen nedenfor). Men derudover kan Fibonacci-sekvensen også bruges som en måde til at måle potentielt vigtige niveauer uden for det nuværende interval. Disse kaldes udvidelsesniveauer (se nummer 2).
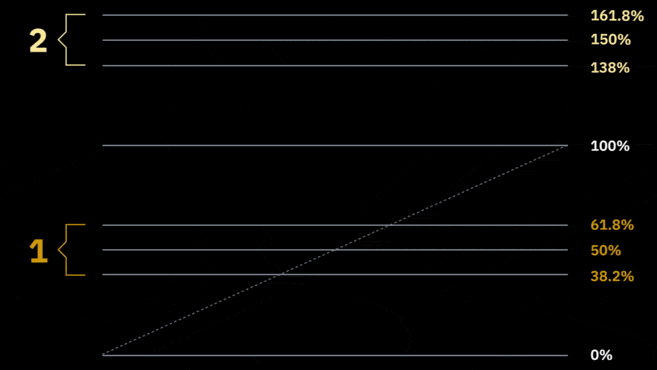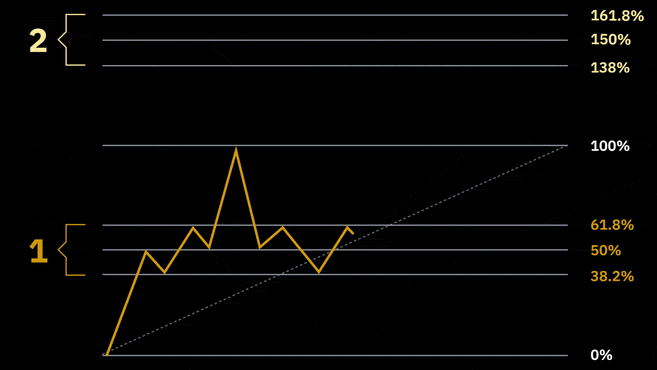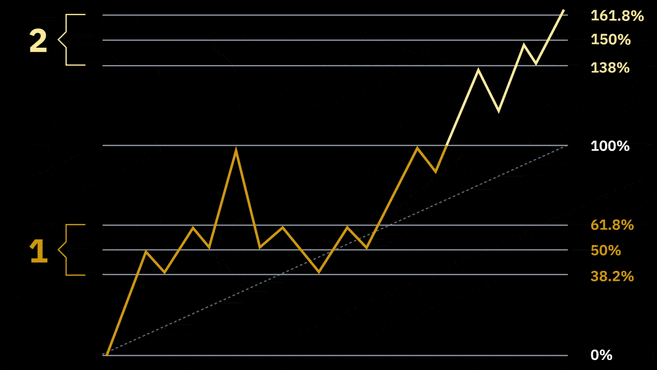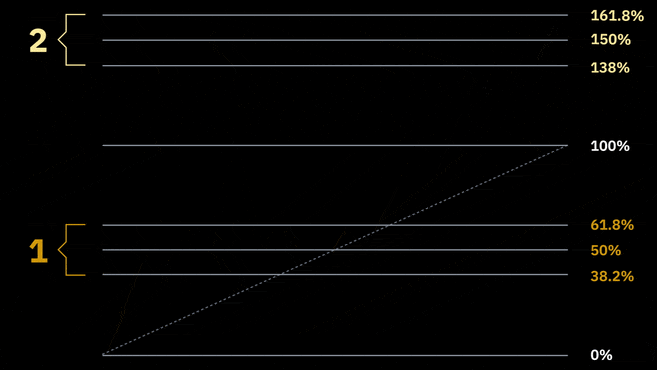
Fibonacci-udvidelsesniveauer kan ses som potentielle handelsmål. Hver handlende kan vælge forskellige udvidelsesniveau som et mål (eller flere mål). De første udvidelsesniveauer er 138,6 %, 150 % og 161,8 % – efterfulgt af 261,8 % og 423,6 %. Så Fibonacci-udvidelsesniveauer kan indikere områder, hvor de næste prisbevægelser kan ende.
Sammenfatning
Fibonacci-tal findes overalt i naturen, og mange handlende mener, at de har relevans, når de kortlægger de finansielle markeder.
Men som med alle tekniske indikatorer er forholdet mellem prisudvikling, grafmønstre og indikatorer ikke baseret på noget videnskabeligt princip eller fysisk lov. Som sådan kan Fibonacci retracement-værktøjets anvendelighed være relateret til antallet af markedsdeltagere, der er opmærksomme på det. Så selvom Fibonacci retracement-niveauer ikke nødvendigvis korrelerer med noget håndgribeligt, kan de fungere som et værktøj til at forsøge at forudsige interesseområder.
